作者:StarkWare 编译:Lu Tian
概述:
- 密码学证明(Cryptographic proofs)在区块链网络中用于验证计算并提高交易的完整性。
- 通过生成可验证的聚合交易证明,L2 区块链实现了可扩展性。
- 零知识证明(ZKP)在不泄露额外信息的情况下验证真实性,但在隐私保护方面的应用存在差异。
- 密码学证明涉及算法化和低强制性等技术方面。
- 随着区块链技术的成熟,某种类型的密码学证明可能成为主导,推动可扩展性、透明度和隐私的发展。
C.S. Lewis将完整性(Integrity )定义为“在无人监视时也能做正确事情”的行为。在区块链背景下,密码学证明用于确保同样的目标,即确保在无人监视的情况下正确执行特定计算过程。
在本文中,我们将探讨密码学证明的概念、它们在区块链中的应用以及实现上的一些关键差异。首先,让我们从定义开始。
什么是密码学证明?
密码学证明是一套数学和密码学协议,用于验证计算的完整性。
一个很好的例子出自1991年的一篇重要论文《对数时间检验计算》( “Checking Computations in Polylogarithmic Time” ),作者为L. Babai、L. Fortnow、L.A. Levin和M. Szegedy。在该论文中,他们提出了一种协议,允许“一台个人电脑监控一群搭载强大但不可靠软件和未经测试硬件的超级计算机的操作”。这意味着具有有限计算能力的设备可以验证一群更强大计算设备的计算完整性,即使操控这些设备的一方恶意或有动机误报计算结果。
区块链中密码学证明的应用实践
过去十年,半实用和实用的证明系统呈爆炸式增长,这些系统具有多种应用,确保计算过程的隐私、安全和完整性。尽管Web2领域同样需要完整性,但由于区块链的开放透明特性以及对数学完整性优先于基于人类完整性的偏好,所有使用通用密码学证明系统的产品都可在Web3,即区块链上找到。为了理解证明如何助力扩展区块链,我们首先需要回顾区块链的工作原理。
当我们在像Solana、Ethereum或Cosmos等区块链上发送交易时,网络中的每个验证者都会收到并执行该交易。这很快会变得效率低下。随着去中心化的发展,包含每笔交易至网络历史记录的计算资源和活动验证者数量呈线性增长。
部分项目(如Aztec、Starknet)通过使用密码学证明来解决这个可扩展性问题。它们被称为第二层有效性Rollup,因为它们处于第一层区块链(如以太坊)之上。L2 Rollup的核心思想是,依靠密码学证明确认链下执行的计算完整性以及状态和交易集合的更新的有效性。对于可验证长时间计算完整性执行,这意味着分布式网络吞吐量的根本变革。一个由众多设备组成的网络可以简单地验证计算步骤,而无需原始地重复执行每个计算步骤。这里不需要超级计算机,一般的低性能计算机即可胜任。
这些庞大计算的完整性验证由第一层网络(如以太坊)的可靠节点执行。在这种情况下,使用1991年论文中预言性语言,L1网络中的验证者扮演“单个可靠的个人电脑”的角色,而L2证明者则是一种超级计算机,令人惊讶的是,在未经测试的硬件和可能不可靠的软件上执行,依然实现了完整性和可靠性。
密码学证明的爆发指的是这些系统在区块链领域的广泛应用以及实施这些证明的不同密码学协议的普及。以下是当前在Web3中使用的众多项目的可视化示例:
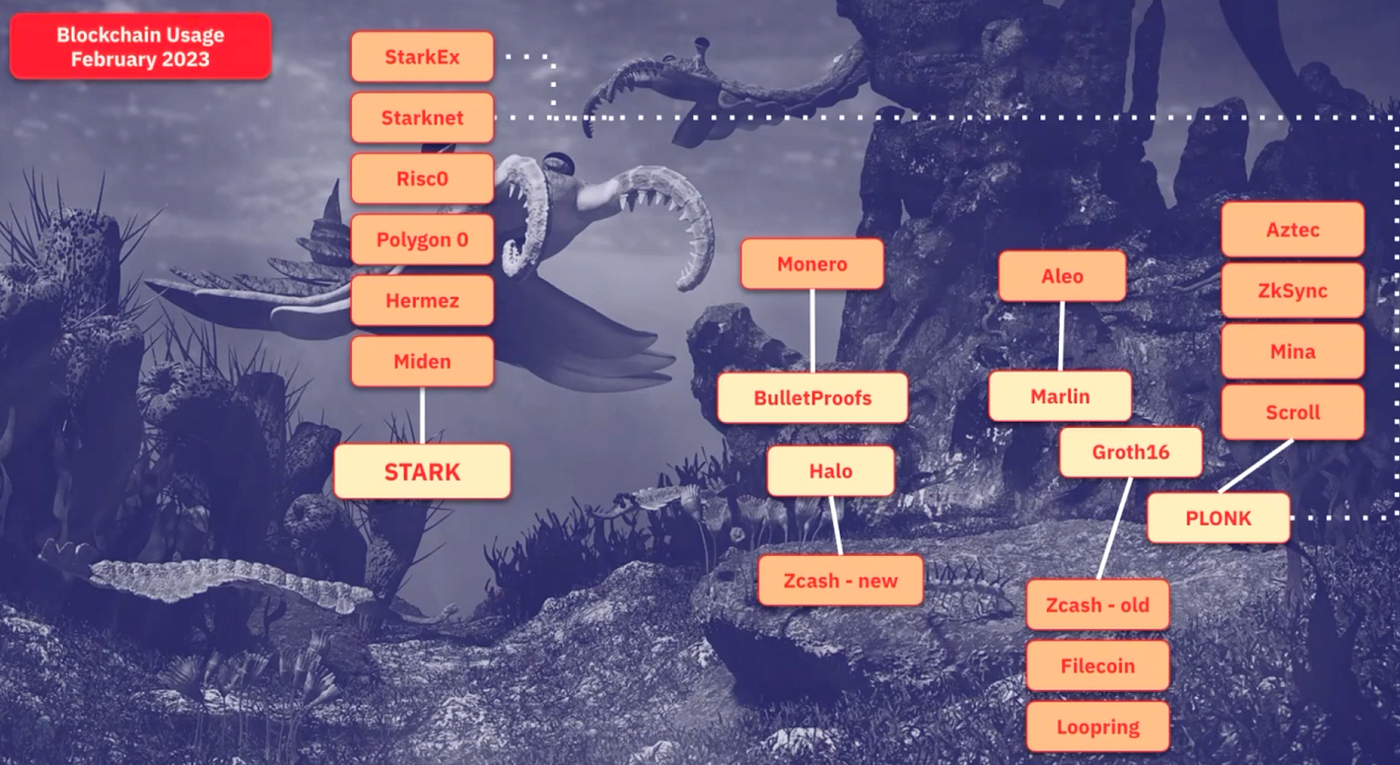
上述项目仅使用了我们所了解的密码学证明系统中的一小部分(至少在理论实现方面)。

比较系统:优缺点解析
在众多选择面前,了解每种实现的优缺点至关重要。尽管许多细节颇具技术性,但掌握这些知识有助于分辨哪些技术可能引领未来的区块链和L2发展。
零知识证明:扩展性与隐私
你可能经常听到一些项目提及“零知识”证明(或ZKP)这一术语。尽管这个词汇颇具吸引力,零知识证明在区块链隐私保护方面具有潜力,但多数Web3 L2有效性Rollup实际上并未使用具备“零知识”密码学属性的证明,而是依赖于密码学证明的可扩展性属性。下面我们简要讨论一下密码学证明中的隐私和可扩展性。
ZKP是一种证明方法,使得一方可以验证特定计算是否正确执行,同时无需揭示该计算所用的输入(如密码、交易财务细节、医疗数据等)。因此,在显著降低验证成本的同时(继承了密码学证明的特性),我们实现了隐私保护。
当一个项目声称使用ZKP时,确切理解其含义至关重要。尽管许多基于区块链的项目宣称采用了“基于ZKP”的技术,但实际上,他们的解决方案并未涉及隐私问题。
通过观察修改后的可视化图像,我们可以看到大部分项目更注重可扩展性而非隐私。
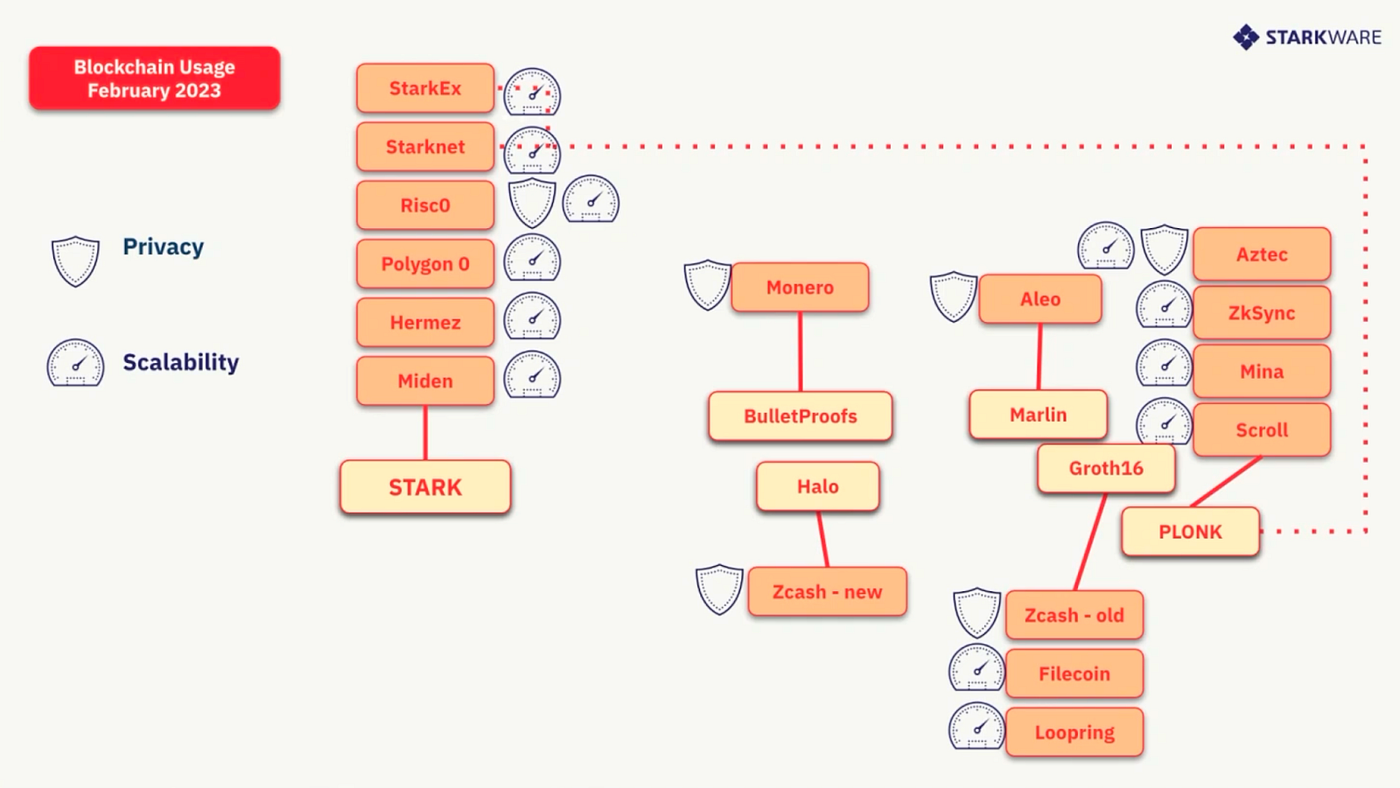
接下来我们将探讨证明中涉及的另外三个技术概念:算术化(arithmetization)、低阶性强制(enforcement of low-degreeness)和密码学假设(cryptographic assumptions)。
算术化是什么?
在研究一个系统需证明的一系列计算时,将这些计算问题转变为代数问题是有意义的。在密码学证明中,算术化指的是利用有限域上的算术运算来表示数学概念和操作的过程。
从宏观角度来看,这意味着将任何陈述表示为代数方程,即多项式。将计算问题转化为这类代数问题的过程在计算机科学术语中被称为“约化(reduction)”。

算术化之所以有助于可扩展性,是因为一旦问题用代数和多项式表示,我们可以提高捕捉完整性违规行为的可能性。为了理解多项式的神奇之处及其在证明中的应用,建议参加STARK 101课程或阅读相关文献。
在研究不同证明系统时,一个区分因素是它们执行算术化的方式。有些系统可能使用整数环(RSA环)上的模运算,而其他系统可能使用椭圆曲线和/或更复杂的方法(基于格的密码学、基于代码的密码学和多元多项式)。
低阶性特征
所有密码学证明系统都采用某种形式的低阶性强制执行,这是它们之间的一个重要区分因素。
低阶性强制执行是确保多项式(作为算术化过程的一部分生成的代数方程式)的阶数低于某个阈值的过程。(提醒一下,多项式的阶数等于其中出现的项的最高次幂。)
低阶性强制执行对完整性和安全性至关重要。如上所述,错误地接受无效证明的概率与所选多项式的阶数相关。此外,这些系统之所以使用低阶多项式,是因为它们具有一些优良的数学性质,使得它们更为高效。
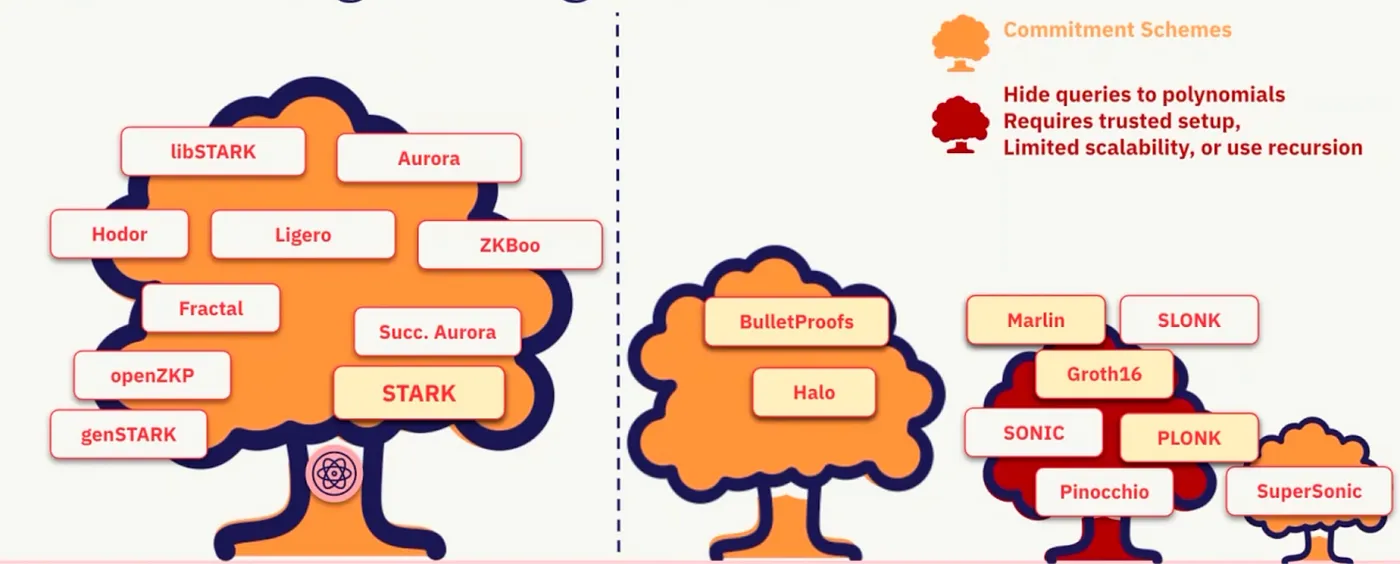
多项式承诺方案(Polynomial Commitment Scheme,PCS)是一种密码学协议,允许在多项式上进行高效且可验证的计算。它使得一方(称为提交者)能够承诺一个多项式而不泄露其完整细节,而另一方(称为验证者)可以随后验证多项式承诺的属性。
不同的证明系统使用不同的多项式承诺方案来创建和验证证明。STARKs和Risc0采用快速Reed-Solomon交互式Oracle证明(Fast Reed-Solomon Interactive Oracle Proof,FRI)承诺方案,而Groth16和PLONK使用KZG承诺方案。总的来说,这些承诺方案之间的区别在于创建证明的成本、验证证明的成本以及证明的大小。
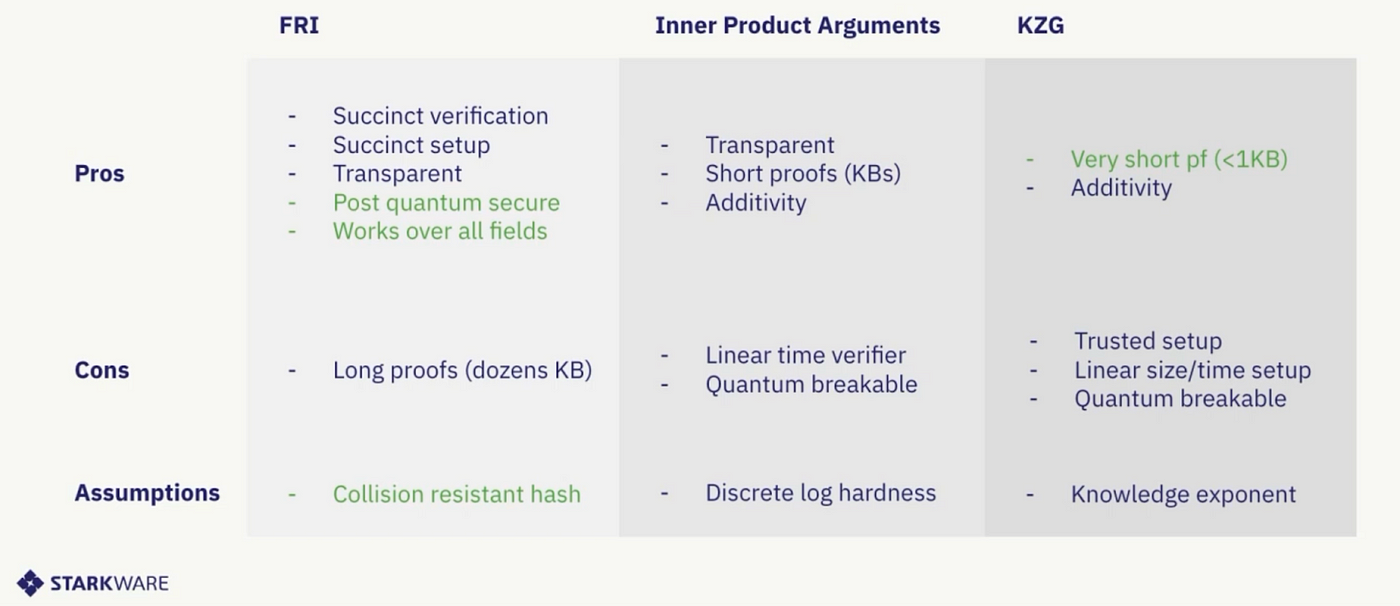
请参照上述图像,了解不同系统的优缺点。STARK证明系统采用FRI协议来强制执行低阶多项式。在这个系统中,证明者与验证者进行交互,承诺新的多项式,使得每个新多项式的阶数是前一个多项式阶数的一半。PLONK系统则使用基于椭圆曲线数学的多项式承诺(例如,KZG)。
此外,某些系统可能需要一个可信设置(trusted setup)。可信设置是一种产生特定私密参数的安排。在这种情况下,挑战在于这些参数的原像必须保持私密。如果不能做到这一点,整个证明系统就会容易受到攻击,伪造证明也将成为可能。
通常来说,会组织特殊的可信设置“仪式”,在此仪式中,多个参与方私下创建随机元素,并将这些元素组合以获得最终的参数。如果有至少一个参与方成功销毁了其提交的随机元素,那么设置可以被认为是安全的。
密码学假设
最后,这些系统所采用的任何其他密码学假设也值得关注。
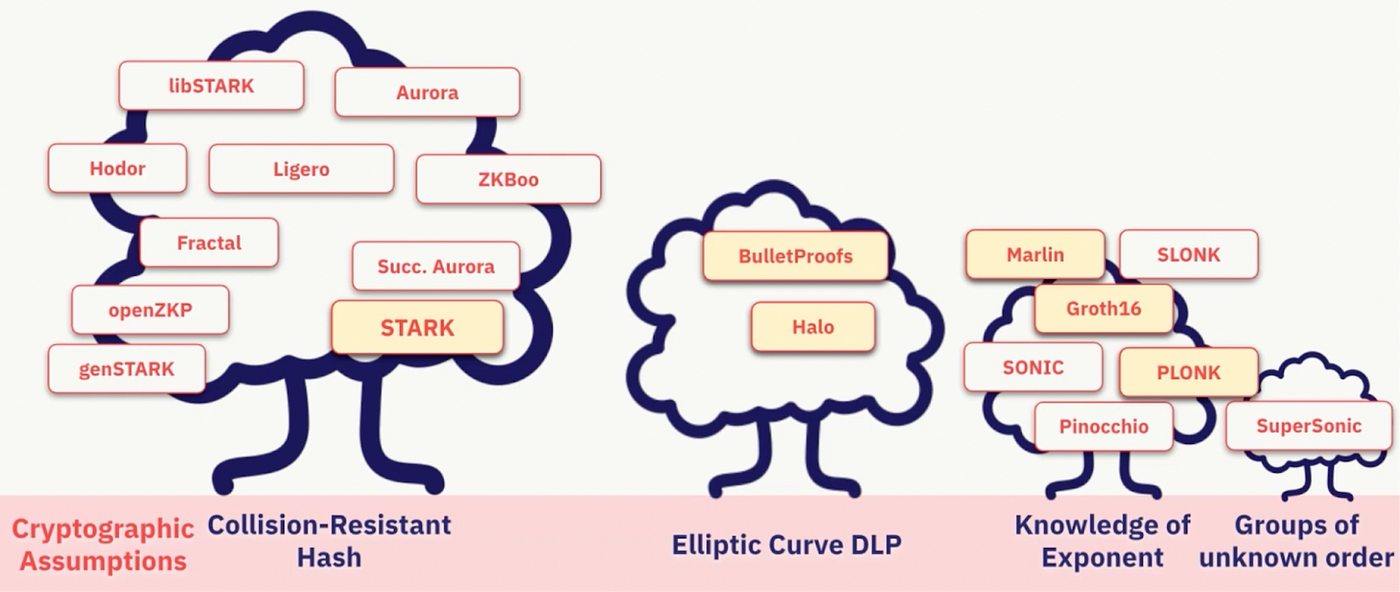
例如,有些系统依赖于椭圆曲线数学(如BulletProofs和Halos)或“指数知识”(如Groth16、PLONK等),而这些是可以被量子计算机破解的。
另一方面,其他系统采用了抵抗量子计算机攻击的哈希函数(如STARKs、ZKBoo等)。
结论
从以上讨论可知,为实现可扩展性和透明性(或隐私),可以采用各种不同的加密证明。尽管某些证明对于简短证明可能非常便捷(如Groth16),但在大型计算中,一些其他系统(如STARKs,在Ben-Sasson教授的观点中)表现更佳。然而,随着生态系统的成熟,我们预期将会有一种加密证明被广泛采用。


所有评论